5.43. numpy – numerical routines for python#
The numpy library is the foundation of the vast majority of scientific computing packages that use Python. It is popular because it provides a greatly simplified interface to complicated algorithms that have fast implementations. Conventional wisdom holds that converting a standard Python program to use numpy will deliver a 10x speedup. In fact, it can be much faster than that. But that’s not the focus of this extremely brief summary of numpy. Instead, we introduce you to the major capabilities and usage patterns that numpy enables. In short, using numpy objects can often eliminated the need for loops entirely. As a consequence, this greatly simplify the algorithms you have to write. So it’s truly worthwhile becoming familiar with this library [3].
numpy is designed for numerical calculation and the primary object the library provides is an array. The array [4] object has several key attributes, including:
Strictly speaking, numpy arrays have type ndarray but they are predominantly created using a top-level array function.
array.ndimattribute, which indicates how many dimensions the array hasarray.shapeattribute, which indicates the number of elements on each dimension.array.dtypeattribute, which indicates the numpy data type [5]. This can also be determined by the input data, or by using thedtypeargument.
numpy extends the range of possible data types, e.g. 8-bit integers, 64-bit floats. See the numpy docs for more details.
5.43.1. Creating an array from existing data#
import numpy
data = numpy.array([0, 1, 2, 3], dtype=int)
data
array([0, 1, 2, 3])
data.ndim
1
data.shape
(4,)
data.dtype
dtype('int64')
Once created, you cannot extend an array, i.e. it’s total number of elements is immutable. However, the array “shape” (and thus dimensions) can be changed and the value at individual coordinates can be changed.
data.resize((2, 2))
data
array([[0, 1],
[2, 3]])
data[0][0] = 42
data
array([[42, 1],
[ 2, 3]])
5.43.2. Conversion to standard python data types#
raw = data.tolist()
raw
[[42, 1], [2, 3]]
5.43.3. Conversion to a different dtype#
There is a method on arrays for converting an array of one type into an array of a different type. For instance
x = numpy.array(["0.12", "0.33"])
x.dtype, x
(dtype('<U4'), array(['0.12', '0.33'], dtype='<U4'))
cast = x.astype(float)
cast.dtype, cast
(dtype('float64'), array([0.12, 0.33]))
So numpy has converted an array of strings into an array of 64-bit precision floats, in one line. Sweet!
5.43.4. Implicit type casting#
The dtype of an array instance dictates what assignment operations mean. For example, say we have an integer array
data.dtype, data
(dtype('int64'),
array([[42, 1],
[ 2, 3]]))
If we try to assign a float to the first element, it will not work because the value is implicitly cast to the dtype of the instance. In this example, only the integer component of the float 5.92132 is assigned.
data[0, 0] = 5.92132
data
array([[5, 1],
[2, 3]])
Warning
Implicit type casting is never what you want! Because numpy does not raise an exception for this case, it is up to the programmer (you) to ensure the array dtype is appropriate. For this example, if you want to be able to assign floats to data you have to convert it to be floats firste, e.g. data.astype(float).
5.43.5. Constructing matrices#
Matrices can be specified on construction by providing, for example, lists of lists. In this example we use a list consisting of two lists, each with 4 elements. This results in a \(2\times4\) array.
data = numpy.array([[0, 1, 2, 3], [4, 5, 6, 7]])
data.shape
(2, 4)
data
array([[0, 1, 2, 3],
[4, 5, 6, 7]])
Or, by combining other arrays [1].
I’ve used the numpy.arange() function, which returns an array object.
a = numpy.arange(4)
a
array([0, 1, 2, 3])
b = numpy.arange(4, 8)
b
array([4, 5, 6, 7])
# from the above numpy arrays
m = numpy.array([a, b])
m
array([[0, 1, 2, 3],
[4, 5, 6, 7]])
5.43.6. Scalar operations on arrays#
A major convenience for arrays is the ability to express element-wise operations as a single statement, instead of having to use a for loop.
Here’s an element-wise addition using a standard for loop on the raw nested list data structure.
5.43.6.1. The laborious (and slow) way#
for i in range(len(raw)):
for j in range(len(raw[i])):
raw[i][j] += 20
raw
[[62, 21], [22, 23]]
5.43.6.2. The simple and fast numpy way#
data += 20
data
array([[20, 21, 22, 23],
[24, 25, 26, 27]])
Nice!
5.43.7. Standard mathematical operations on arrays#
If two or more arrays have the same shape, then element-wise operations between corresponding elements is also very simply expressed.
print("Before:", a, b, sep="\n")
c = a * b
print("After:", c, sep="\n")
Before:
[0 1 2 3]
[4 5 6 7]
After:
[ 0 5 12 21]
If they do not have a compatible shape, a ValueError exception is raised and the text indicates “… operands could not be broadcast together with shapes…”.
d = numpy.arange(5)
a * d
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[20], line 2
1 d = numpy.arange(5)
----> 2 a * d
ValueError: operands could not be broadcast together with shapes (4,) (5,)
5.43.8. Array iteration#
Behaves the same as iterating over a standard Python list (or tuple) with the same dimensions. This corresponds to iterating over axis=0.
for e in data:
print(e)
[20 21 22 23]
[24 25 26 27]
5.43.9. Indexing and slicing#
In the following, we are working on this array.
array([[20, 21, 22, 23],
[24, 25, 26, 27]])
We can select an individual element using the standard looking slice notation.
data[0][1]
np.int64(21)
Note that each dimension requires successive [] pairs. The numpy extended slicing notation allows using one set of [].
data[0, 1]
np.int64(21)
The slicing capabilities of arrays is rich and very useful! We can slice a matrix for a single column across all rows
data[:, 1] # the [1] column
array([21, 25])
or a single row across all columns. In both cases the : represents the complete set.
data[1, :] # the [1] row
array([24, 25, 26, 27])
5.43.10. Ensuring array shapes are compatible for mathematical operations#
There are rules that numpy uses to determine how arrays are broadcast together. The best resource to understanding this is the official documentation on broadcasting. That said, here’s a very condensed explanation.
When the array shapes are not the same, numpy compares the shapes element wise from right to left. The dimensions of two arrays are considered compatible when they are same or one of them is 1. Consider the arrays x and y
x = numpy.array([[0, 1], [2, 3], [4, 5], [6, 7]])
x
array([[0, 1],
[2, 3],
[4, 5],
[6, 7]])
x.shape
(4, 2)
y = numpy.array([1, 5, 9, 13])
y
array([ 1, 5, 9, 13])
y.shape
(4,)
Applying the broadcast rule, these are incompatible.
1x * y
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[31], line 1
----> 1 x * y
ValueError: operands could not be broadcast together with shapes (4,2) (4,)
This is because, the first value read from the right of x.shape is 2 and from the right of y.shape is 4.
For our example, one solution that ensures the result of the * operation has the same shape as x is to add a “new axis” to y. This can be done via a combination of slicing and using numpy.newaxis
x * y[:, numpy.newaxis]
array([[ 0, 1],
[10, 15],
[36, 45],
[78, 91]])
or, equivalently, by explicitly reshaping y.
x * y.reshape((4,1))
array([[ 0, 1],
[10, 15],
[36, 45],
[78, 91]])
We could also solve this using the transpose x (which flips the matrix, reversing it’s dimensions)
x.T * y
array([[ 0, 10, 36, 78],
[ 1, 15, 45, 91]])
but this has the effect of meaning the result is also transposed with respect to the original orientation, which is typically inconvenient.
5.43.11. Array assignment#
Consider the following data.
a = numpy.array([[38, 28, 93], [96, 95, 70]])
l = a.tolist()
Assignment to individual elements of an array is more flexible than the comparable standard python objects. For instance, to assign 0 to all values of a is simply
a[:] = 0
a
array([[0, 0, 0],
[0, 0, 0]])
Trying that on a list, however, raises an exception.
1l[:] = 0
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In[37], line 1
----> 1 l[:] = 0
TypeError: must assign iterable to extended slice
As the exception indicates, looping is required.
We can assign to an individual element using the numpy notation.
data[1, 2] = -99
data
array([[ 20, 21, 22, 23],
[ 24, 25, -99, 27]])
5.43.12. Evaluation operations#
Using standard python evaluation operations on numpy arrays returns element wise bool arrays. We show uses for these below.
indices = data < 0
indices
array([[False, False, False, False],
[False, False, True, False]])
5.43.13. Advanced indexing#
There are two types of advanced indexing, boolean and integer.
5.43.13.1. Boolean indexing#
This applies when the object being used to slice the array is of type bool. These typically result from some array comparison operation.
m = numpy.array([[1, 2], [-3, 4], [5, -6]])
m
array([[ 1, 2],
[-3, 4],
[ 5, -6]])
Let’s identify all elements that are \(<0\).
negative = m < 0
negative
array([[False, False],
[ True, False],
[False, True]])
The result is an array with boolean elements indicating whether the corresponding value in m satisfied (indicated by True) or not (indicated by False) the condition (\(<0\)). We can use bool arrays to slice the others with the same shape.
m[negative]
array([-3, -6])
As this shows, using a bool array for indexing on the original returns just those elements as a flat array. If you want your operation to generate a result with the same shape you need to “index in place”. For instance, you can use the index to restrict specific operations to just those elements represented by the index such as this assignment statement.
m[negative] = 0
m
array([[1, 2],
[0, 4],
[5, 0]])
5.43.13.2. Integer indexing#
This involves as many series of integers as there are dimensions to the array (e.g. 2 in the case of m).
Before we start using actual integer series, I’ll start by using conventional indexing to get the value of a single item. Specifically, I select row 1, column 1.
row_index = 1
col_index = 1
m[row_index, col_index]
np.int64(4)
We now enclose those indices in lists, such that each successive value corresponds to another row, another column. As such these sequential arrays correspond to array coordinates and thus must have the same dimension (length in our example below).
row_indices = [1, 2, 0]
col_indices = [1, 0, 1]
m[row_indices, col_indices]
array([4, 5, 2])
This corresponds to the following array coordinates: (1, 1), (2, 0), (0, 1). Thus, the returned value from advanced indexing is an array with same length as the indexing array length (3 in our case).
5.43.14. The numpy array axis#
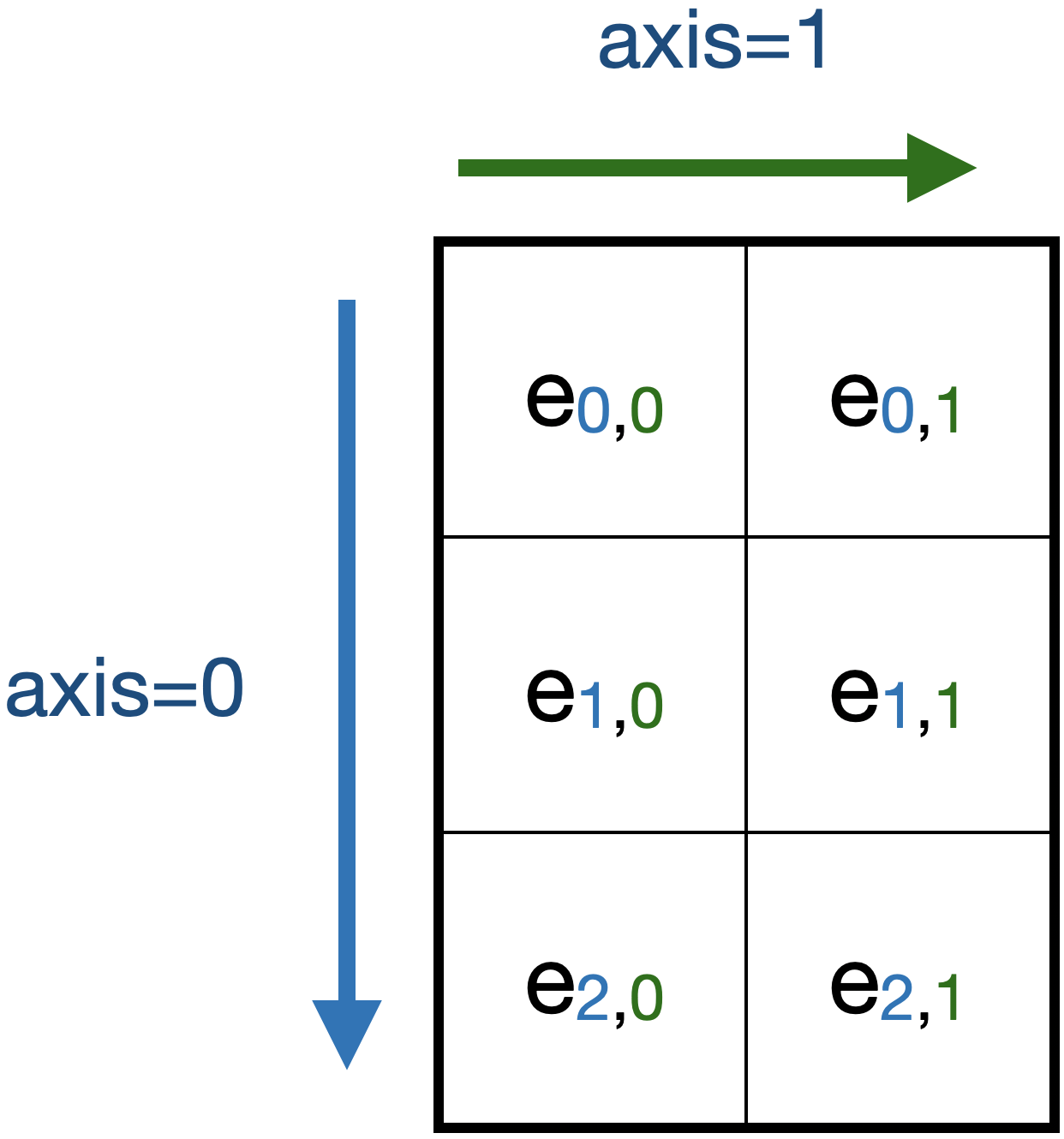
An array with shape=(3,2), ndim=2. Elements and their array indices are shown as e\(_{i,j}\). Many array methods have an axis argument that applies to arrays with ndim>1. In the illustrated example, setting axis=0 would apply that method along the corresponding axis and generate a result with 2 elements. Setting axis=1 would generate a result with 3 elements.
As illustrated, the axis argument specifies whether a method / function operates on rows or columns [2].
You can have many more than 2-dimensions with arrays. More dimension means you have more axes and thus larger values of axis may be required.
Working on this array.
array([[ 20, 21, 22, 23],
[ 24, 25, -99, 27]])
data.sum(axis=0)
array([ 44, 46, -77, 50])
5.43.15. Getting useful statistical quantities#
# Overall mean, all elements
data.mean()
np.float64(7.875)
# Unbiased estimate of standard deviation, all elements
data.std(ddof=1)
np.float64(43.24163833291109)
# Column means, operating on rows
data.mean(axis=0)
array([ 22. , 23. , -38.5, 25. ])
# Row means, operating on columns
data.mean(axis=1)
array([21.5 , -5.75])
5.43.16. Linear algebra – matrix multiplication#
Matrix multiplication is a fundamental operation in linear algebra and is central to many statistical procedures (e.g. fitting linear models, taking the exponential of a matrix, likelihood of a phylogeny).
data1 = numpy.array([0, 1, 2, 3])
data2 = numpy.array([4, 5, 6, 7])
ip = numpy.inner(data1, data2)
ip
np.int64(38)
The @ symbol also serves as a special operator for matrix multiplication.
data1 @ data2
np.int64(38)
5.43.17. Conditionals on arrays#
Conditional operations on numpy arrays are important. We illustrate the utility of these operations with some simple examples.
data = numpy.array([[1, 2, 1, 9], [9, 1, 1, 3]])
matched = data > 3
matched
array([[False, False, False, True],
[ True, False, False, False]])
The above expression is evaluated element wise and returns a numpy array of type bool.
We use the standard Python in operator.
if 3 in data:
print("Yes")
else:
print("No")
Yes
We apply a conditional to an array and use the any() method, which will return True if any single element satisfied this condition.
if (data > 3).any():
print("Yes")
else:
print("No")
Yes
Using the all() method, which will return True only if all elements satisfied the condition.
if (data > 3).all():
print("Yes")
else:
print("No")
No
5.43.18. Comparisons of multiple arrays#
numpy provides tools for element-wise comparisons. This is more complicated than just using the standard python syntax.
x = numpy.array([True, False, False, True], dtype=bool)
y = numpy.array([False, False, False, True], dtype=bool)
Applying equivalence operators to arrays can result in exceptions because the result is ambiguous.
x or y
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[59], line 1
----> 1 x or y
ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()
Instead, you should use special functions which will operate element wise. Here’s a couple of examples.
numpy.logical_or(x, y)
array([ True, False, False, True])
numpy.logical_and(x, y)
array([False, False, False, True])
5.43.19. Using the result of array comparisons to count#
Scenario, you want to count (from multiple arrays that consist of a continuously distributed random variable) the number of times a specific threshold is reached for each “position” on a reference coordinate system.
data = [
numpy.array([0.923, 0.022, 0.360, 0.970, 0.585]),
numpy.array([0.480, 0.282, 0.055, 0.873, 0.960]),
]
# create an array that will be used to count how often
# a certain threshold is met
counts = numpy.zeros((5,), dtype=int)
counts
array([0, 0, 0, 0, 0])
print(data[0] > 0.5)
for da in data:
counts[da > 0.5] += 1
counts
[ True False False True True]
array([1, 0, 0, 2, 2])
data = numpy.array(data)
(data > 0.5).sum(axis=0)
array([1, 0, 0, 2, 2])
5.44. Exercises#
Create a list of 10 positive integers and convert it into a
numpyarray. Usearraymethods to compute the total. Divide the original array by the total to produce a normalised array, which you assign to a variablefreqs. Usingnumpylogical operations to show that all elements are between 0 and 1. Use array methods to show the array sum is 1.Many methods on
numpyarrays have anaxisargument, one of which issum(). Construct a 2-dimensional (2D) array that has the same number of rows and columns, e.g.[[0, 0], [0, 0]]
is a 2D array. Assign values that make it easy to distinguish operations that operate across rows versus those which operate across columns [6]. Demonstrate this matrix serves that purpose using
sum().booldata types can be summed. Create a sample array withdtype=booland show that the sum of this array equals the number of occurrences ofTrue.Look at the array
dataand identify the array coordinates where the values equal 9. Now use advanced array indexing to extract those coordinates in a single line statement.data = numpy.array([[1, 9, 0, 3, 9], [9, 2, 8, 2, 1], [3, 1, 9, 9, 5]])
The result should be
array([9, 9, 9, 9, 9])
Same as the previous question except in a single line statement extract the values ≠9. The result should be
array([1, 0, 3, 2, 8, 2, 1, 3, 1, 5])
Use boolean array indexing to assign -3 to all values of
dataless than 2. The result should bearray([[-3, 9, -3, 3, 9], [ 9, 2, 8, 2, -3], [ 3, -3, 9, 9, 5]])For the following boolean array
indices, what is the result of~indices?indices = numpy.array([True, True, False, True], dtype=bool)
Convert the following code into using
numpy– withoutforloops. After convertingcountsto anumpyarray, my solution is 3 lines long.from math import log10 counts = [[-4, 3, 4, -3, 4], [4, -1, -2, -3, 4], [-4, -1, 2, 0, 3], [2, -2, -2, -4, -5]] result = [] for i in range(4): row = [] for j in range(4): val = counts[i][j] val = 0 if val <= 0 else log10(val) row.append(val) result.append(row) result
[[0, 0.47712125471966244, 0.6020599913279624, 0], [0.6020599913279624, 0, 0, 0], [0, 0, 0.3010299956639812, 0], [0.3010299956639812, 0, 0, 0]]
array([[0. , 0.47712125, 0.60205999, 0. , 0.60205999], [0.60205999, 0. , 0. , 0. , 0.60205999], [0. , 0. , 0.30103 , 0. , 0.47712125], [0.30103 , 0. , 0. , 0. , 0. ]])What happens when you slice the following 1D array using
newaxison the first axis, or the second axisx = numpy.array([1, 9, 0, 3, 9])
Comparing performance of pure Python and
numpyimplementations. Investigate usage ofnumpy.where()to obtain the row and column coordinates of a 2D array where the value equals1(that’s a one). Write a function callednp_where()that takes a matrix as an argument and returns the row coordinates and column coordinates.First, use the following code to generate a random square matrix.
from numpy.random import randint dim = 5 mat = randint(0, 2, size=dim * dim) mat.resize(dim, dim) mat
array([[1, 1, 1, 0, 0], [1, 0, 0, 1, 0], [1, 1, 0, 1, 1], [1, 1, 1, 0, 0], [1, 0, 1, 1, 0]])Compare
np_where()to the performance of a function implemented using only pure python calledpy_where()that takes the matrix as an argument and returns the<row coordinates>, <column coordinates>as lists. Format, it should return the following.([0, 0, 0, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4, 4], [0, 1, 2, 0, 3, 0, 1, 3, 4, 0, 1, 2, 0, 2, 3])
Use the “magic”
%timeitcommand builtin to Jupyter to assess performance of each function on the same value ofmat.%timeit py_where(mat)
7.17 μs ± 75.5 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
Then try setting
dim=20and repeat. Which is faster, and by how much?Do some googling for testing
numpyarrays usingassert_allclose. Then use this to check your arrayfreqscreated above sums to 1.
You want the sum of rows to be different to the sum of columns, that way you know when you have used axis correctly.