7.5. Mutation – the origin of genetic variation

Mutation manifests as a change in the primary DNA [1] sequence of an organism. Only mutations that occur within the cell lineage that produce sex cells, the germline, can have an influence on future generations. We refer to these as germline mutations.

What happens to a mutation?

This process only applies to the germ cells.

In the side bar, we present a cartoon representation of the possible events that can affect a new genetic variant. The process begins at a single DNA molecule within a single cell as a lesion, a chemical change that disrupts the double-helix. If that lesion reverts to its original form or is correctly repaired by a DNA repair process, then we do not observed any change in the sequence. If this new variant is not transmitted to the next generation, then we never see it. If it does get transmitted, then it can be “lost” from the population purely by chance due to the process known as random genetic drift [2]. If the variant is deleterious, it may be lost as a consequence of natural selection eliminating the individuals that carry it, thus preventing them from contributing to the next generation. Finally, a variant that survives all of that can attain a frequency of 1.0 in a species. We apply the term substitution here since the original variant present in all members of a species has been substituted with this derived variant.

[1]

Of course, some viruses use RNA for the genome, but we limit ourselves to DNA here.

[2]

If the variant survives to a sufficient population frequency, we refer to it as a polymorphism. Polymorphic means “many forms”. In terms of genetic variation, this is most often presented as SNPs (single nucleotide polymorphisms) or the largely synonymous term SNV (single nucleotide variant). The latter terms is probably better, since the original definition for polymorphism applied only to loci for which the minor allele frequency was \(\ge 0.01\) (and before that \(\ge 0.05\)). Since increase capacity to survey genetic variation, those arbitrary cutoffs have less value.

Any process that influences the different stages in a characteristic manner will contribute to the characteristics of the distribution of genetic variation.

7.5.1. Types of mutation

There are a 3 main mutation types.

Point mutations

The state of a single nucleotide changes between parent and daughter DNA sequence. The daughter DNA molecule is the same length as the parent.

Deletions

Deletions of DNA range in scale from single nucleotides to large genomic segments. The daughter DNA molecule is shorter than the parent.

Insertions

Range in scale from single to multiple nucleotides up to large genomic segments. The daughter DNA molecule is longer than the parent.

Within each of these, there are substantial sub-categories. We are interested in insertion / deletion events (indels) insomuch as they motivate the need for sequence alignment algorithms. Our principal focus, however, is on point mutation processes since those are the dominant type of genetic variation data.

7.5.2. Point mutations

There are 12 distinct point mutation events since each nucleotide can mutate to 3 possible alternates (e.g. A\(\rightarrow\)C, A\(\rightarrow\)G, A\(\rightarrow\)T). These are often categorised by the chemical classes of the bases involved. Specifically, transitions and transversions. Point mutations that start and end in bases belonging to the same chemical class are referred to as transitions, i.e. changes involving A\(\rightarrow\)G, G\(\rightarrow\)A, C\(\rightarrow\)T, T\(\rightarrow\)C (blue lines in the figure). The remaining changes are assigned to the transversion category. As it turns out, there are differences in the rate at which mutations of these categories are observed, and it has been argued that the excess of transitions reflects the chemical properties of DNA [TF76].

Mutation directions

The different point mutations.

The blue lines indicate transition mutations, point mutations between bases that belong to the same chemical class – between the purines (A/G) or pyrimidines (C/T).

The dominance of transition mutations reflects more than just the intrinsic properties of the canonical bases. The modified base 5-methyl-cytosine (hereafter ⁵mC or methylated cytosine) is present in vertebrates and many other organisms. In vertebrates, at least, this modification can be used to encode information – switching between methylated and unmethylated states is associated with changes to gene expression of flanking genes. As such, ⁵mC is a part of the epigenetic control layer. The modified base ⁵mC is also hypermutable [CMFG78]. The deamination of ⁵mC (a hydrolysis reaction) occurs at a rate ~10x the same reaction of unmethylated C. The lesion arising from these reactions also differ, with ⁵mC producing T while hydrolysis of unmethylated C produces uracil (U). These lesions cause a pairing mismatch in the helix, triggering DNA repair mechanisms. As U is typically seen in RNA we might reasonably expect a repair system will do a better job of reverting U:G to the correct C:G compared with resolving a T:G mismatch.

Where ⁵mC mutagenesis gets even more interesting is that this is an enzymatically induced modification and the recognition sequence for the DNA methylase is a C followed by a G, denote CpG (the p stands for the phosphodiester bond between adjacent nucleotides). This sequence “context dependent” introduction of the base modification therefore results in a context dependence of C\(\rightarrow\)T point mutations (see Sidebar Figure).

Context dependence of C\(\rightarrow\)T point mutations

Information analysis of human intergenic SNPs resulting from a C\(\rightarrow\)T point mutation [ZNYH17].

RE is relative entropy. Position is relative to the point mutation (at 0). The normal letter orientation in the plot indicates that base was over-represented in mutant sequences compared to the reference distribution. The rotated orientation indicates that base was under-represented in mutant sequences.

7.5.3. Statistical measures of sequence composition that relate to mutation

As the C\(\rightarrow\)T case illustrates, chemical and metabolic processes affect how mutation occurs. To further illustrate this, we consider an additional property of DNA sequences – strand.

When we discuss processes via which lesions form in DNA, we are predominantly referencing chemical reactions affecting the base part of a nucleotide. Thymidine dimers arise from UV light induced covalent bonds between Thymine bases that are physically adjacent on the same DNA strand. This strand orientation leads to a simple question: Does mutation occur in a strand symmetric way?

To address this, let’s think back to what we actually observe. We do not observe the mutation process, we observe the outcome [3]. Let’s assume we detect a G\(\rightarrow\)A difference between the parent DNA sequence and its immediate descendant. We represent DNA sequences by picking one strand and displaying that information only [4], often an entirely arbitrary choice. Accordingly, the designation of mutation direction is also arbitrary and, for our example, its possible this mutation was in fact a C\(\rightarrow\)T on the other strand. If the mutation was of CpG→CpA, it’s likely the actual mutation involved the ⁵mC on the opposite strand since CpG is a strand symmetric dinucleotide (the reverse complement is also CpG).

Let’s consider a though experiment in where we run a mutagenesis experiment for a very long time on DNA that does not encode any information. In the absence of any biochemical biases, we expect mutation processes to occur with equal probability on the two strands. As a consequence, we expect at chemical equilibrium, the bases that form the canonical Watson-Crick base pairs to have equals counts on the strand, i.e. they are strand-symmetric. For instance, the DNA sequence ATGC is strand symmetric, as is AATTGC. The following “Skewness” statistics are used to quantify strand symmetry (or strand parity).

\[ \begin{align}\begin{aligned}S_{AT} = \frac{A-T}{A+T}\\S_{GC} = \frac{G-C}{G+C}\end{aligned}\end{align} \]

These divide the difference in the counts of the Watson-Crick pairs by their total. If sequence mutation has predominantly operated in a strand-symmetric manner throughout time, the expected value of both \(S_{AT}\) and \(S_{GA}\) is 0 [5].

We present two figures from published work that prove strikingly informative. The first concerns the putative influence of initiating DNA replication from a fixed location. It is conjectured that the distinct nature of DNA synthesis on leading versus lagging strands drives the appearance of striking asymmetries in some bacterial genomes [MrazekK98].

[3]

Except in specific experimental contexts.

[4]

Because of the Watson-Crick base-pairing rules, the other strand can be deduced and thus presenting it is redundant.

[5]

The order of the base counts in the statistics can differ between publications.

The influence of DNA replication

Bacillus subtilis genome.

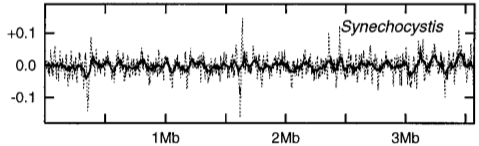
Synechocystis PCC6803 genome.

Panels copied from Figure 1 of [MrazekK98]. The \(y\)-axis is \(-S_{GC}\) computed from a 50kb sliding window across the corresponding genome. The statistic is assigned to the middle base of thew window. The arrow indicates the origin of replication.

The second example concerns the distribution of strand symmetry around genes in humans [TNA+03]. In this case, the proposed biochemical mechanism is transcription coupled DNA repair. In simplistic terms, this is a DNA damage repair system that is induced by a stalled RNA polymerase. The repair has been shown to be limited to the transcribed strand. This observation implies that the non-transcribed strand receives less scrutiny by lesion repair processes. This asymmetry also manifests in the SNPs that are present in humans today, indicating the influence is active [SH20].

Transcription associated mutation asymmetries

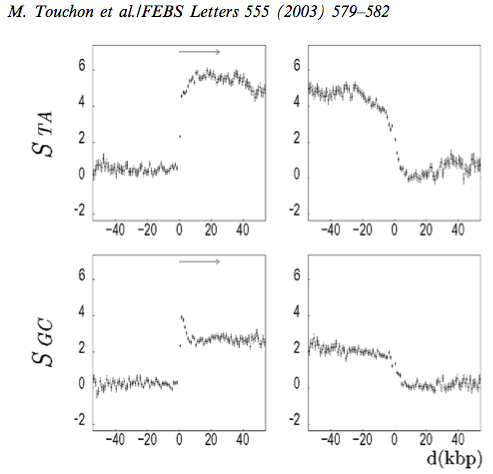
Statistics were calculated using the human genome sequence in 1kb windows around genes. The left column shows the transcriptional start site (TSS) at index 0. The \(x\)-axis values correspond to distances to the TSS in the left column. In the right column they correspond to the distance from the 3`-terminus of the annotated gene transcript. The \(y\)-axis values are the mean skew statistic for that position from all human genes.

Copied from Figure 3 of [TNA+03].

---

Citations

[CMFG78]

C Coulondre, J H Miller, P J Farabaugh, and W Gilbert. Molecular basis of base substitution hotspots in \emp Escherichia coli. Nature, 274:775–780, 1978.

[MrazekK98] (1,2)

Jan Mràzek and Samuel Karlin. Strand compositional asymmetry in bacterial and large viral genomes. Proceedings of the National Academy of Sciences of the United States of America, 95:3720–3725, 1998. URL: www.pnas.org., doi:10.1073/pnas.95.7.3720.

[SH20]

Helmut Simon and Gavin Huttley. Quantifying Influences on Intragenomic Mutation Rate. G3: Genes|Genomes|Genetics, 10:g3.401335.2020, 2020. URL: https://doi.org/10.1534/g3.120.401335, doi:10.1534/g3.120.401335.

[TF76]

M D Topal and J R Fresco. Complementary base pairing and the origin of substitution mutations. Nature, 263:285–289, 1976.

[TNA+03] (1,2)

M Touchon, S Nicolay, A Arneodo, Y D'Aubenton-Carafa, and C Thermes. Transcription-coupled TA and GC strand asymmetries in the human genome. FEBS Lett, 555:579–582, 2003.

[ZNYH17]

Yicheng Zhu, Teresa Neeman, Von Bing Yap, and Gavin A Huttley. Statistical methods for identifying sequence motifs affecting point mutations. Genetics, 205:843–856, 2017. doi:10.1534/genetics.116.195677.